RRT* Examples
LQR-RRT* with Linear Dynamics
The LQR-RRT* algorithm can be run with linear dynamics using the following.
1def lin_lqrrrtstar():
2 import numpy as np
3
4 import gncpy.dynamics.basic as gdyn
5 import gncpy.control as gctrl
6 from gncpy.planning.rrt_star import LQRRRTStar
7
8 SEED = 29
9
10 start_time = 0
11 dt = 0.01
12
13 rng = np.random.default_rng(SEED)
14
15 # define dynamics
16 dynObj = gdyn.DoubleIntegrator()
17 pos_inds = [0, 1]
18 dynObj.control_model = lambda _t, *_args: np.array([[0, 0], [0, 0], [1, 0], [0, 1]])
19 u_nom = np.zeros((2, 1))
20 state_args = (dt,)
21
22 # define starting and ending state
23 end_state = np.array([0, 2.5, 0, 0]).reshape((4, 1))
24 start_state = np.array([0, -2.5, 0, 0]).reshape((4, 1))
25
26 # define some circular obstacles with center pos and radius (x, y, radius)
27 obstacles = np.array(
28 [
29 [0, -1.35, 0.2],
30 [1.0, -0.5, 0.2],
31 [-0.95, -0.5, 0.2],
32 [-0.2, 0.3, 0.2],
33 [0.8, 0.7, 0.2],
34 [1.1, 2.0, 0.2],
35 [-1.2, 0.8, 0.2],
36 [-1.1, 2.1, 0.2],
37 [-0.1, 1.6, 0.2],
38 [-1.1, -1.9, 0.2],
39 [1.0 + np.sqrt(2) / 10, -1.5 - np.sqrt(2) / 10, 0.2],
40 ]
41 )
42
43 # define enviornment bounds
44 minxy = np.array([-2, -3])
45 maxxy = np.array([2, 3])
46 search_area = np.vstack((minxy, maxxy))
47
48 # define the LQR planner
49 lqr = gctrl.LQR()
50 Q = 50 * np.eye(len(dynObj.state_names))
51 R = 0.6 * np.eye(u_nom.size)
52 lqr.set_cost_model(Q, R)
53 lqr.set_state_model(u_nom, dynObj=dynObj, dt=dt)
54
55 # define the state sampler for the LQR-RRT* object
56 def sampling_fun(rng, pos_inds, min_pos, max_pos):
57 out = np.zeros((len(dynObj.state_names), 1))
58 out[pos_inds] = rng.uniform(min_pos.ravel(), max_pos.ravel()).reshape((-1, 1))
59
60 return out
61
62 # Initialize LQR-RRT* Planner
63 lqrRRTStar = LQRRRTStar(rng=rng, sampling_fun=sampling_fun)
64 lqrRRTStar.set_environment(search_area=search_area, obstacles=obstacles)
65 lqrRRTStar.set_control_model(lqr, pos_inds)
66
67 # Run Planner
68 trajectory, cost, u_traj, fig, frame_list = lqrRRTStar.plan(
69 start_time,
70 start_state,
71 end_state,
72 use_convergence=True,
73 state_args=state_args,
74 disp=True,
75 plt_inds=[0, 1],
76 show_animation=True,
77 save_animation=True,
78 provide_details=True,
79 )
80
81 return frame_list
which gives this as output.
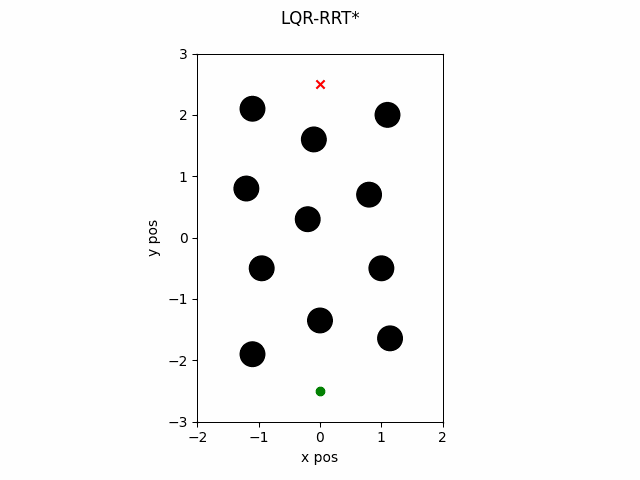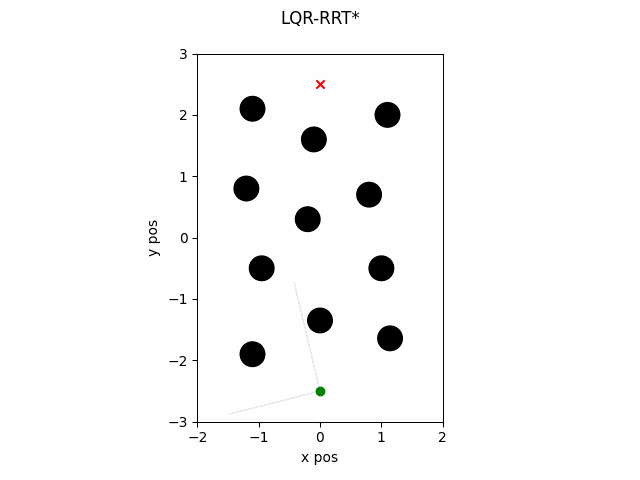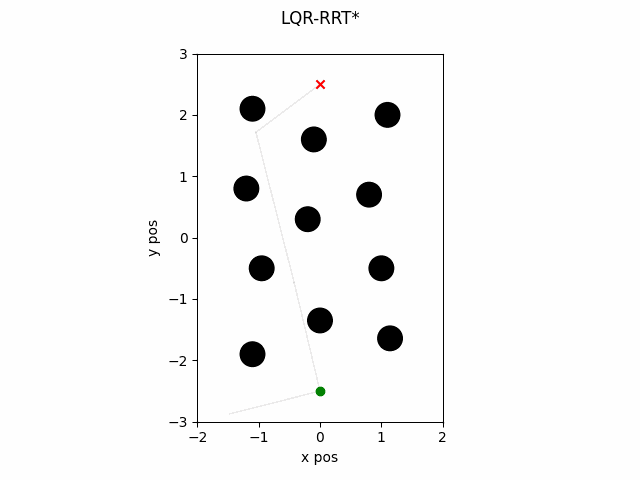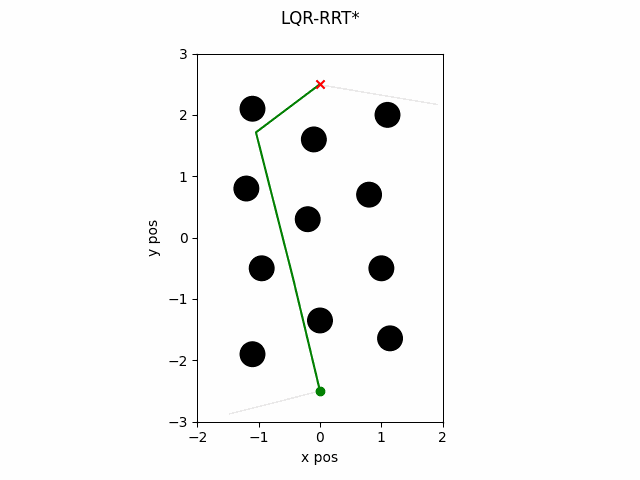
LQR-RRT* with Non-Linear Dynamics
The LQR-RRT* algorithm can be run with non-linear dynamics using the following.
1def nonlin_lqrrrtstar():
2 import numpy as np
3
4 import gncpy.dynamics.basic as gdyn
5 import gncpy.control as gctrl
6 from gncpy.planning.rrt_star import LQRRRTStar
7
8 d2r = np.pi / 180
9 SEED = 29
10
11 start_time = 0
12 dt = 0.01
13 time_horizon = 100 * dt
14
15 rng = np.random.default_rng(SEED)
16
17 # define dynamics
18 dynObj = gdyn.CurvilinearMotion()
19 pos_inds = [0, 1]
20
21 u_nom = np.zeros((2, 1))
22
23 # define starting and ending state
24 ang = 90 * d2r
25 vel = 0
26 start_state = np.array([0, -2.5, vel, ang]).reshape((-1, 1))
27 end_state = np.array([0, 2.5, vel, ang]).reshape((-1, 1))
28
29 # define some circular obstacles with center pos and radius (x, y, radius)
30 obstacles = np.array(
31 [
32 [0, -1.35, 0.2],
33 [1.0, -0.5, 0.2],
34 [-0.95, -0.5, 0.2],
35 [-0.2, 0.3, 0.2],
36 [0.8, 0.7, 0.2],
37 [1.1, 2.0, 0.2],
38 [-1.2, 0.8, 0.2],
39 [-1.1, 2.1, 0.2],
40 [-0.1, 1.6, 0.2],
41 [-1.1, -1.9, 0.2],
42 [1.0 + np.sqrt(2) / 10, -1.5 - np.sqrt(2) / 10, 0.2],
43 ]
44 )
45
46 # define enviornment bounds
47 minxy = np.array([-2, -3])
48 maxxy = np.array([2, 3])
49 search_area = np.vstack((minxy, maxxy))
50
51 # define the LQR planner
52 lqr = gctrl.LQR(time_horizon=time_horizon)
53 Q = np.diag([50, 50, 0.01, 0.1])
54 R = np.diag([0.0001, 0.001])
55 lqr.set_cost_model(Q, R)
56 lqr.set_state_model(u_nom, dynObj=dynObj, dt=dt)
57
58 # define the state sampler for the LQR-RRT* object
59 def sampling_fun(rng, pos_inds, min_pos, max_pos):
60 out = np.zeros((len(dynObj.state_names), 1))
61 out[pos_inds] = rng.uniform(min_pos.ravel(), max_pos.ravel()).reshape((-1, 1))
62
63 # sample velocity to make sure its not 0
64 bnd = 1
65 ii = 2
66 out[ii] = rng.uniform(-bnd, bnd)
67 while out[ii] < 1e-8:
68 out[ii] = rng.uniform(-bnd, bnd)
69
70 # sample turn angle to make sure its not 0
71 bnd = 5 * d2r
72 ii = 3
73 out[ii] = rng.uniform(ang - bnd, ang + bnd)
74 while out[ii] < 1e-8:
75 out[ii] = rng.uniform(ang - bnd, ang + bnd)
76
77 return out
78
79 # Initialize LQR-RRT* Planner
80 lqrRRTStar = LQRRRTStar(rng=rng, sampling_fun=sampling_fun)
81 lqrRRTStar.set_environment(search_area=search_area, obstacles=obstacles)
82 lqrRRTStar.set_control_model(lqr, pos_inds)
83
84 # Run Planner
85 trajectory, cost, u_traj, fig, frame_list = lqrRRTStar.plan(
86 start_time,
87 start_state,
88 end_state,
89 use_convergence=True,
90 disp=True,
91 plt_inds=[0, 1],
92 show_animation=True,
93 save_animation=True,
94 provide_details=True,
95 ttl="Non-Linear LQR-RRT*",
96 )
97
98 return frame_list
which gives this as output.
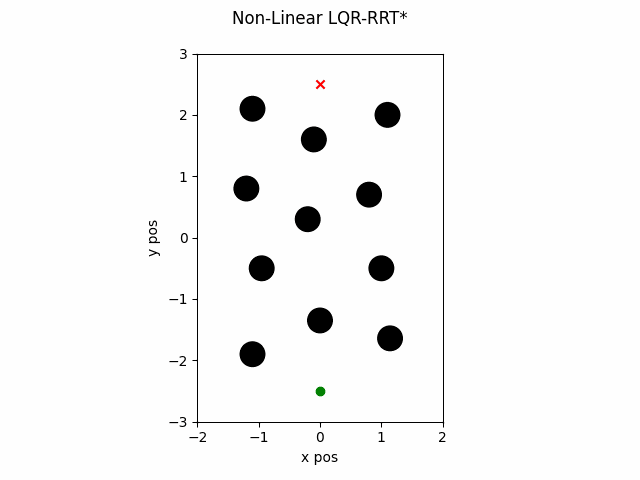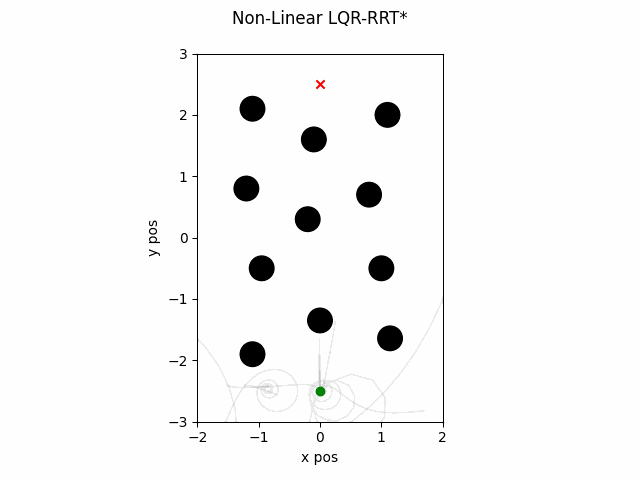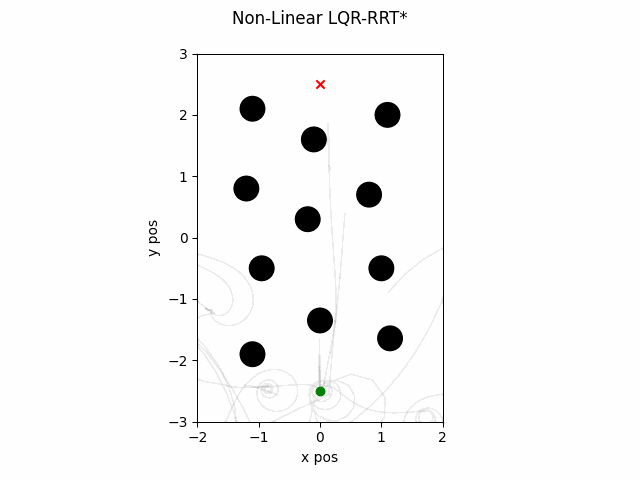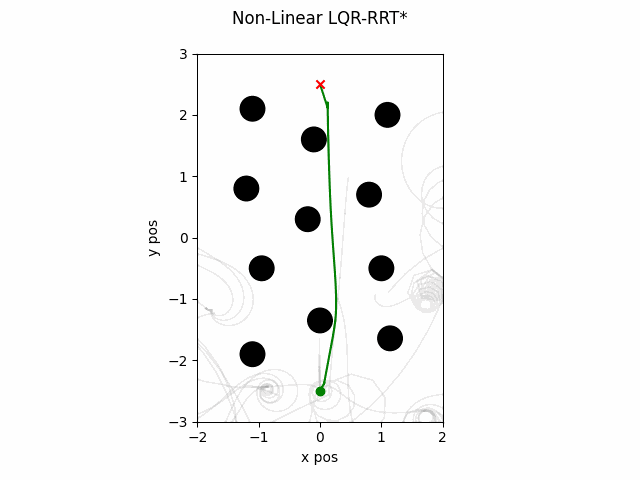
ELQR-RRT* with Non-Linear Dynamics
The ELQR-RRT* algorithm can be run with non-linear dynamics using the following.
1def elqrrrtstar():
2 import numpy as np
3
4 import gncpy.dynamics.basic as gdyn
5 import gncpy.control as gctrl
6 from gncpy.planning.rrt_star import ExtendedLQRRRTStar
7
8 d2r = np.pi / 180
9 SEED = 29
10
11 start_time = 0
12 dt = 0.01
13 time_horizon = 100 * dt
14
15 rng = np.random.default_rng(SEED)
16
17 # define dynamics
18 dynObj = gdyn.CurvilinearMotion()
19 pos_inds = [0, 1]
20
21 u_nom = np.zeros((2, 1))
22
23 # define starting and ending state
24 ang = 90 * d2r
25 vel = 0
26 start_state = np.array([0, -2.5, vel, ang]).reshape((-1, 1))
27 end_state = np.array([0, 2.5, vel, ang]).reshape((-1, 1))
28
29 # define some circular obstacles with center pos and radius (x, y, radius)
30 obstacles = np.array(
31 [
32 [0, -1.35, 0.2],
33 [1.0, -0.5, 0.2],
34 [-0.95, -0.5, 0.2],
35 [-0.2, 0.3, 0.2],
36 [0.8, 0.7, 0.2],
37 [1.1, 2.0, 0.2],
38 [-1.2, 0.8, 0.2],
39 [-1.1, 2.1, 0.2],
40 [-0.1, 1.6, 0.2],
41 [-1.1, -1.9, 0.2],
42 [1.0 + np.sqrt(2) / 10, -1.5 - np.sqrt(2) / 10, 0.2],
43 ]
44 )
45
46 # define enviornment bounds
47 minxy = np.array([-2, -3])
48 maxxy = np.array([2, 3])
49 search_area = np.vstack((minxy, maxxy))
50
51 # define the LQR controller
52 controller = gctrl.ELQR(time_horizon=time_horizon, max_iters=300, tol=1e-2)
53 controller_args = dict()
54 Q = np.diag([50, 50, 4, 2])
55 R = np.diag([0.05, 0.001])
56
57 obs_factor = 1
58 scale_factor = 1
59 cost_args = (obstacles, obs_factor, scale_factor, minxy, maxxy)
60
61 def non_quadratic_cost(
62 tt,
63 state,
64 ctrl_input,
65 end_state,
66 is_initial,
67 is_final,
68 _obstacles,
69 _obs_factor,
70 _scale_factor,
71 _bottom_left,
72 _top_right,
73 ):
74 radius = 0
75 cost = 0
76 # cost for obstacles
77 for obs in _obstacles:
78 diff = state.ravel()[pos_inds] - obs[0:2]
79 dist = np.sqrt(np.sum(diff * diff))
80 # signed distance is negative if the robot is within the obstacle
81 signed_dist = (dist - radius) - obs[2]
82 if signed_dist > 0:
83 continue
84 cost += _obs_factor * np.exp(-_scale_factor * signed_dist).item()
85
86 # add cost for going out of bounds
87 for ii, b in enumerate(_bottom_left):
88 dist = (state[pos_inds[ii]] - b) - radius
89 cost += _obs_factor * np.exp(-_scale_factor * dist).item()
90
91 for ii, b in enumerate(_top_right):
92 dist = (b - state[pos_inds[ii]]) - radius
93 cost += _obs_factor * np.exp(-_scale_factor * dist).item()
94
95 return cost
96
97 # define modifications for quadratizing the cost function
98 def quad_modifier(itr, tt, P, Q, R, q, r):
99 rot_cost = 0.4
100 # only modify if within the first 2 iterations
101 if itr < 2:
102 Q[-1, -1] = rot_cost
103 q[-1] = -rot_cost * np.pi / 2
104
105 return P, Q, R, q, r
106
107 controller.set_cost_model(Q=Q, R=R, non_quadratic_fun=non_quadratic_cost, quad_modifier=quad_modifier)
108 controller.set_state_model(u_nom, dynObj=dynObj, dt=dt)
109
110 # define the state sampler for the LQR-RRT* object
111 def sampling_fun(rng, pos_inds, min_pos, max_pos):
112 out = np.zeros((len(dynObj.state_names), 1))
113 out[pos_inds] = rng.uniform(min_pos.ravel(), max_pos.ravel()).reshape((-1, 1))
114
115 # sample velocity to make sure its not 0
116 bnd = 1
117 ii = 2
118 out[ii] = rng.uniform(0.1, bnd)
119 while out[ii] < 1e-8:
120 out[ii] = rng.uniform(-bnd, bnd)
121
122 # # sample turn angle to make sure its not 0
123 out[3] = ang
124
125 return out
126
127 # Initialize ELQR-RRT* Planner
128 elqrRRTStar = ExtendedLQRRRTStar(rng=rng, sampling_fun=sampling_fun)
129 elqrRRTStar.set_environment(search_area=search_area, obstacles=obstacles)
130 elqrRRTStar.set_control_model(controller, pos_inds, controller_args=controller_args)
131
132 # Run Planner
133 trajectory, cost, u_traj, fig, frame_list = elqrRRTStar.plan(
134 start_time,
135 start_state,
136 end_state,
137 cost_args=cost_args,
138 disp=True,
139 plt_inds=pos_inds,
140 show_animation=True,
141 show_planner=True,
142 save_animation=True,
143 provide_details=True,
144 ttl="ELQR-RRT*",
145 )
146
147 return frame_list
which gives this as output.